

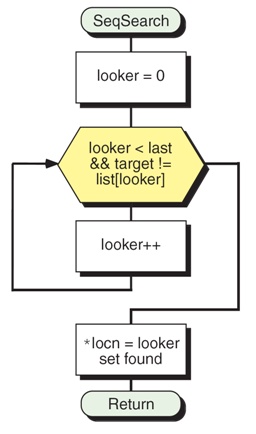
Before a comparison between the target item and a list item can be performed, the list item must be selected. Of course, these numbers don’t tell the whole story. A sequential search of a seven item list requires 3.5 comparisons, on average, for successful searches and 7 comparisons for unsuccessful searches. In fact, no more than three comparisons will ever be needed in a binary search of a seven item list. Note that in either case, only three comparisons were required to determine whether the target item was in the original seven item list. Illustrates two examples of binary search on a seven item list – one successful, the other unsuccessful. With an N of 8, position 5 would be designated as the “middle” position. When N = 7, position 4 would be designated as the “middle” position. Where ⌊⌋, read “floor”, means that fractions should be dropped. The process of determining the position of the “middle” item in a list of N items can be expressed mathematically as: In this case, the very next item following the midpoint (which falls between items) is chosen as the “middle” item. If the list is composed of an even number of items, then there is no item in the exact middle of the list. If the number of items in the list is odd, then there is a well-defined middle item. - the items following, but not including, the middle itemīinary search depends on being able to quickly determine which item is in the middle of the list of remaining items.repeat this entire procedure on the second half of the list.If the current item is smaller than the target item then - the items up to, but not including, the middle item.repeat this entire procedure on the first half of the list.If the current item is larger than the target item then If the current item is the same as the target item then
Let the current item be the item in the middle of the list The binary search algorithm is presented formally in. After three steps the list is only 1/8 the original size. After the second step, if the target item is in the list but has not yet been found, its location will have been narrowed to a list that is ¼ the size of the original list. This process may be repeated until either: (1) the target item is found, or (2) the list of remaining items is empty. But, what should be done next? The answer is to repeat this process on the new list: select the middle item of the new list, compare it to the target item, and if it does not match discard half the items in that list. The second half of the list – the middle item and everything after it – could be dropped.Īfter performing this first step, the current list would be half the size of the original list. If the middle item had been larger than the target, then the target could only occur in the first half of the list. Hence, the first half of the list – everything up to and including the middle item – can be safely discarded without an exhaustive examination of each of the items in that portion of the list. Since the search list was presorted, if the target item occurs anywhere in the list, it must be after the midpoint. Let’s say that the middle item is smaller than the target item. Clearly, if the target item is the same as the middle item, then the algorithm has found the item it was looking for and can print the “Yes, found it.” message and halt. Essentially, binary search begins by jumping to the midpoint of the search list and comparing the item it finds there to the target item it is searching for. It is much more efficient than sequential search, but requires that the search list be presorted. However, for large lists, sorting even once can be so expensive that simply performing a sequential search from the start may be the best choice.Binary search is another approach to the search problem. If we can sort once and then search many times, the cost of the sort is not so significant. In fact, we should always consider whether it is cost effective to take on the extra work of sorting to gain searching benefits. We leave this implementation as an exercise.Įven though a binary search is generally better than a sequential search, it is important to note that for small values of n, the additional cost of sorting is probably not worth it. Luckily this can be remedied by passing the list along with the starting and ending indices. This means that the binary search using slice will not perform in strict logarithmic time. However, we know that the slice operator in Python is actually $\mathcal(n)$. The analysis that we did above assumed that the slice operator takes constant time. Uses the slice operator to create the left half of the list that is then passed to the next invocation (similarly for the right half as well). In the recursive solution shown above, the recursive call, One additional analysis issue needs to be addressed.


 0 kommentar(er)
0 kommentar(er)
